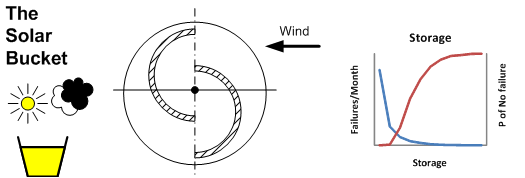
A common measure of sustainability is the percentage of energy generated from renewable resources such as wind, solar, tidal, hydro, bio-mass etc. Often the time period on which this statistic is estimated is a year. Equally important is the timing of supply and demand. The classic example is solar generation, the graph below illustrates the demand for electricity on a typical spring day and the solar irradiance available to contribute to meeting it, a similar graph could be drawn for wind and the time period extended to include seasonal variations.
The two ways of meeting the overnight demand are storage and alternative means of generation. Most energy economies are evolving to adapt to diverse means of generation. At the present time it is hard to make a good case for storage as most energy economies can absorb what wind and solar installations can offer them and frequently, they are given priority when working out how to meet demand. In general, there are few surpluses of energy which can be accumulated in a storage system, even if such a system is available. I don't have a handle on the relative risks and economics of utility scale storage and generation, but at a guess, maintaining a fossil/nuclear generating capability is the "low" risk option. The approach makes wind and solar sources incremental parts of the energy mix which need backing up with an equivalent amount of conventional capacity.
The case for storage is that it is a step towards sustainability. At its most basic, the harvest from solar panels during the day can be stored and used to keep the lights on after dark. Within the arid regions towards the equator, where there a clear skies and relatively small seasonal variations, this could be a workable scenario. In the temperate regions, more complex system are needed with a mix of solar and wind. Solar works well in summer, but the winter yields are low, wind works better in winter and on some days neither produce very much.
I'm currently messing with a very small scale storage project in which a small computer attempts to keep itself alive by "buying" sustainable energy, this could be done as a computer similar (which is happening as a parallel task), but the having some hardware, makes it both fun (other relevant words are frustrating and expensive) and more instructive than a bunch of numbers from a computer programme. There in one economic nicety, you can attempt to use off-peak electricity which is approx. 7p/kwh where possible in preference to normal daytime rates which are close to 20p/kwh. If you used this approach to ensure that a high proportion of the electricity you use was from renewable resources, you would have some capital and operating costs beyond those normally associated with turning the lights on.
Living next to a railway station used by commuters, I've become aware that there are an increasing number of electric cars around, typically, these are priced at around £20k after a £5k government subsidy. Apart from their high cost, electric vehicles charged by off-peak electricity are an attractive concept, in effect they are storage on wheels. An interesting policy study would be the effect of providing similar support for including storage into homes and offices.
Friday, 28 March 2014
Friday, 21 March 2014
Clouds and Irradiance - A Simple Model
Simulating the performance of a solar energy system requires a model for solar irradiance. Solar irradiance is a function of Sun-Earth geometry and atmospheric conditions of which cloud cover is the most significant. On a typical summer day in the south of England there will be a few or scattered cumulus clouds which might reduce the global horizontal irradiance to 80% of its clear sky level, whilst in winter a thick layer of stratus can reduce this to 10 - 20%.
As with everything else on this blog, this is unreviewed work-in-progress and should be treated with caution. This is post is a simplified description of a project, it is planned to compile a more detailed account of the work at a later date.
The basis of the model is the attenuation of clear sky irradiance caused by the presence of clouds, this is described by a variable called the clear sky factor (CSF) which is defined as:
The graph below was compiled from data collected around noon in June 2011 illustrates the variation in CSF with cloud cover. for the clear sky it constant at 1.00, for overcast conditions it is more or less constant at approximately 0.15. On a day of scattered cumulus cloud the CSF fluctuated widely, the low levels recorded when the cloud passed between the measuring device and the sun, the CSF was close to that of the overcast sky, during the period of transition between cloud and clear sky, the CSF exceeded 1.0 due to an increase in diffuse irradiance, this might be called the cloud fringe effect.
GHI was chosen as a measure of irradiance because it is the most commonly collected form of irradiance data. A basic measuring device is simply a small horizontally mounted PV cell. Clear sky irradiance is influenced by factors such a aerosols and water vapour, whilst there are some excellent models which take these into account, for most locations little is known about the state of the atmosphere at a specific time, especially when clouds are present in the sky. After some experimentation, a correlation developed by the Meinells which requires only air mass as an input was found to produce a reasonable estimate of Direct Normal Irradiance (DNI). GHI is a combination of direct normal irradiance and diffuse horizontal irradiance (DHI), as no equivalent formula to the Meinell one could be found for diffuse irradiance, one was derived from local observations using a simple shaded radiometer, this latter formula is subject to revision as more data becomes available.
In the south of England, the "economic" range of air mass is approximately 1.2 to 6.0, for these values the plane parallel formula for Air Mass produces a workable estimate and offers some computational convenience. This simplification may not be appropriate for regions such as Arizona where there is significant DNI at much higher values of air mass.
The formulas used for the estimated clear sky GHI are:
- FEW - up to 2 octas
- SCaTtered - 3 - 4 octas
- BroKeN - 5 - 7 octas
- OVerCast - 8 octas, no blue sky visible
One way of creating a model it use distributions of CSF for a given cloud extent. The graphs below are summaries of the effect of low cloud (less than 6,000 feet) in a maritime temperate climate, also known as Sussex of Cfb in the Koppen system of climate classification. The distributions for few, scattered and broken cloud are typically bimodal. the low mode describes the CSF when the sun is obscured by cloud and the high mode is the interval of clear sky between the passage of clouds.
When there are only a few clouds in the sky, the average value of CSF is around 0.8 and there is a greater probability of high values of CSF (i.e. the overall attenuation is small).
As the extent of the cloud increases, the average value of CSF falls for scattered clouds and the probability of CSF being either high or low is approximately equal. This is consistent with the definition of scattered cloud which is that up to half the sky contains cloud.
Part of the definition of broken cloud is that there is at least some blue sky visible even though most of the sky is full of cloud, this is reflected in the summary graph.
There is no blue sky visible under an overcast sky and the distribution is unimodal and the mean is low.
These summaries are over simplifications designed to allow a simple model. Other factors which are important are the height of the equivalent summaries cloud, high cloud are significantly different and the values of CSF much greater. The model as currently configured, simply takes the highest, and most dense layer, which effectively assumes a simple sky, often the sky is complex, especially during the passage of fronts. Part of the work in progress is to determine the variation in attenuation between climates, for example the nature of solar irradiance in the desert regions of Arizona, are significantly different from those on the south coast of England.
Friday, 14 March 2014
I'd like to call this research.....
But its also having fun with a kite.
The kite was given to me as a Christmas present by my son (aged 23 at the time, him not me). It's a small kite which fits easily into a pocket and would be ideal for business people. One can imagine herding the participants of a meeting into the car park and sending the kite aloft. Then point upwards and exclaim "that's were we should be", followed by a profound silence and the sensible one saying "shall we go back inside now?".
Despite a complete lack of electronics and telemetry, the kite gives an insight into the the nature of wind at heights between 5 and 25 metres (maybe higher, I replaced the original string with a longer one and its still climbing). Last Saturday when the wind was blowing 3 - 4 m/s, I took the kite to two different locations. The first was a beach where the wind was coming in off the sea and the second was a public park in an urban area a mile or so north of the seafront. The behaviour of the kite was significantly different at each site.
On the beach, the kite effortlessly took to the air and was stable at a height of 5m and the trailing streamers had no difficulty in keeping it head up to the wind. Once the string was fully unwound, the kite sat comfortably in the sky, maybe with the odd flutter, but I was able to hook the handle on to the bike and take the photo at the top of the page. After half an hour, I felt guilty about bringing it back to Earth.
At the park, things were different. I almost pointed out to the man mowing the cricket pitch who cast disapproving looks in my direction, that what he was going to do on the grass later in the day was no less ridiculous than what I was doing but life's too short for pointless conversations. Here the kite struggled with turbulence up to, say, 15m and getting it airborne required many attempts, hoping that it would acquire enough upward motion to counter any downward influences. With patience, it was possible to get the string fully extended, but the kite was never stable and was prone to twisting and each twist tied a small knot in the string. I suggest that the number of knots in a kite string is a measure of wind turbulence. Nor did the kite stay aloft. Typically in urban areas, wind is not a smooth stream of air, but a series of gusts, often with significant gaps between then, it was in these gaps that the kite spiralled to the ground. The kite suggested that conditions measured at 2m, extend upwards to at least 25m. It was also clear that wind speed increased with height, even though the turbulence persisted.
When the next opportunity presents itself, I will take the kite into the hills to the north of the town, just because its fun.
PS - 18-Apr-2014 - I found myself on the same beach yesterday, this time the wind was coming from the NE and was blowing from the land to the sea. The turbulence that is observable inland made it hard to get the kite airborne and once aloft, it started to drift earthwards as soon as a gust had subsided.
The kite was given to me as a Christmas present by my son (aged 23 at the time, him not me). It's a small kite which fits easily into a pocket and would be ideal for business people. One can imagine herding the participants of a meeting into the car park and sending the kite aloft. Then point upwards and exclaim "that's were we should be", followed by a profound silence and the sensible one saying "shall we go back inside now?".
Despite a complete lack of electronics and telemetry, the kite gives an insight into the the nature of wind at heights between 5 and 25 metres (maybe higher, I replaced the original string with a longer one and its still climbing). Last Saturday when the wind was blowing 3 - 4 m/s, I took the kite to two different locations. The first was a beach where the wind was coming in off the sea and the second was a public park in an urban area a mile or so north of the seafront. The behaviour of the kite was significantly different at each site.
On the beach, the kite effortlessly took to the air and was stable at a height of 5m and the trailing streamers had no difficulty in keeping it head up to the wind. Once the string was fully unwound, the kite sat comfortably in the sky, maybe with the odd flutter, but I was able to hook the handle on to the bike and take the photo at the top of the page. After half an hour, I felt guilty about bringing it back to Earth.
At the park, things were different. I almost pointed out to the man mowing the cricket pitch who cast disapproving looks in my direction, that what he was going to do on the grass later in the day was no less ridiculous than what I was doing but life's too short for pointless conversations. Here the kite struggled with turbulence up to, say, 15m and getting it airborne required many attempts, hoping that it would acquire enough upward motion to counter any downward influences. With patience, it was possible to get the string fully extended, but the kite was never stable and was prone to twisting and each twist tied a small knot in the string. I suggest that the number of knots in a kite string is a measure of wind turbulence. Nor did the kite stay aloft. Typically in urban areas, wind is not a smooth stream of air, but a series of gusts, often with significant gaps between then, it was in these gaps that the kite spiralled to the ground. The kite suggested that conditions measured at 2m, extend upwards to at least 25m. It was also clear that wind speed increased with height, even though the turbulence persisted.
When the next opportunity presents itself, I will take the kite into the hills to the north of the town, just because its fun.
PS - 18-Apr-2014 - I found myself on the same beach yesterday, this time the wind was coming from the NE and was blowing from the land to the sea. The turbulence that is observable inland made it hard to get the kite airborne and once aloft, it started to drift earthwards as soon as a gust had subsided.
Friday, 7 March 2014
The Rayleigh Distribution
One of the reasons for modelling a system is to get an understanding of how it might work before you build it, the logic being that paper are spreadsheets are cheap whilst metal and earth moving are expensive. There are many ways of doing this, one is to use historic data as the input, for example a time series of wind speed measurements, another is use some form maths/stats function to mimic the real world. Each approach has its strengths and weaknesses.
I'm currently messing with a storage based project, some initial work was done on a computer, but to make it a bit more fun, I'm building a very small prototype which is controlled by weather reports from the internet. This provides some insights which a purely maths and stats approach would hide, not the least of these is the economics of the process. In a mathematical model, changing a parameter is often just a matter of editing a line of code, with a physical model, changing something usually involves a cycle ride and spending money. This has forced some decisions on how much information is needed to drive the system and what is nice-to-have which leads to a discussion on the merits of a big budget which allows flexibility and experimentation or a small budget in which constraints may foster creativity. Such is life at the cutting edge of R and D.
As with anything on this blog, this is unreviewed work in progress which should be treated with caution.
When I first became interested in sustainable energy systems, I found a source of data which provided the average wind speed for a given location. the figure for my backyard was 5.0 m/s (I think), this might be the case for level ground devoid of trees and houses, but it was a start. To make an estimate of the energy that might be extracted from a stream of moving air, it is necessary have a distribution of the wind speed. One solution is to use the Rayleigh distribution, which with the help of spreadsheet can take an average wind speed and turn it into a histogram which is an estimate of the of the number of hours per year a given wind speed will occur. The Rayleigh distribution is a special case of the Weibull in which the shape factor is fixed at 2.0 which simplifies the process. Both the Rayleigh and Weibull distributions can be used to model wind speed. The relationship between the maths and the wind is empirical which simply means "it works" without a providing a causal mechanism. This sort of model is common in science, the goals scored in a football match can follow a Poison distribution, rainfall can follow a Gamma distribution, extremes can be described with the Pareto and Gumbel distributions (amongst others).
The graph below shows the distribution of wind speed which is estimated by the Rayleigh model and observed wind speed for a selected location with an average wind speed of 5 ms/s:
In this case, there is reasonable agreement between the estimated and observed values, in part because the dataset was chosen for this reason.
As part of a project to learn about the nature of wind as an energy source, I collected data from diverse location, which I'm still studying. The inference from this, so far, is that the Rayleigh distribution describes the wind speed distribution at an "ideal" location. It provides a reasonable model where the terrain is flat or a plateau and also for offshore wind in locations poleward of the tropics and for upper air soundings at the 850 mb level. It does not provice a good model where the terrain is complex or for urban areas. In these cases, a better solution might be to use a Weibull distribution where the shape factor is in the range 1.2 to 1.8. In these cases, the Rayleigh distribution will over estimate the energy yield.
This is a link to a more detailed description of the Rayleigh Distribution, it will be updated over the next few weeks as other work is completed.
Rayleigh Distribution
I'm currently messing with a storage based project, some initial work was done on a computer, but to make it a bit more fun, I'm building a very small prototype which is controlled by weather reports from the internet. This provides some insights which a purely maths and stats approach would hide, not the least of these is the economics of the process. In a mathematical model, changing a parameter is often just a matter of editing a line of code, with a physical model, changing something usually involves a cycle ride and spending money. This has forced some decisions on how much information is needed to drive the system and what is nice-to-have which leads to a discussion on the merits of a big budget which allows flexibility and experimentation or a small budget in which constraints may foster creativity. Such is life at the cutting edge of R and D.
As with anything on this blog, this is unreviewed work in progress which should be treated with caution.
When I first became interested in sustainable energy systems, I found a source of data which provided the average wind speed for a given location. the figure for my backyard was 5.0 m/s (I think), this might be the case for level ground devoid of trees and houses, but it was a start. To make an estimate of the energy that might be extracted from a stream of moving air, it is necessary have a distribution of the wind speed. One solution is to use the Rayleigh distribution, which with the help of spreadsheet can take an average wind speed and turn it into a histogram which is an estimate of the of the number of hours per year a given wind speed will occur. The Rayleigh distribution is a special case of the Weibull in which the shape factor is fixed at 2.0 which simplifies the process. Both the Rayleigh and Weibull distributions can be used to model wind speed. The relationship between the maths and the wind is empirical which simply means "it works" without a providing a causal mechanism. This sort of model is common in science, the goals scored in a football match can follow a Poison distribution, rainfall can follow a Gamma distribution, extremes can be described with the Pareto and Gumbel distributions (amongst others).
The graph below shows the distribution of wind speed which is estimated by the Rayleigh model and observed wind speed for a selected location with an average wind speed of 5 ms/s:
In this case, there is reasonable agreement between the estimated and observed values, in part because the dataset was chosen for this reason.
As part of a project to learn about the nature of wind as an energy source, I collected data from diverse location, which I'm still studying. The inference from this, so far, is that the Rayleigh distribution describes the wind speed distribution at an "ideal" location. It provides a reasonable model where the terrain is flat or a plateau and also for offshore wind in locations poleward of the tropics and for upper air soundings at the 850 mb level. It does not provice a good model where the terrain is complex or for urban areas. In these cases, a better solution might be to use a Weibull distribution where the shape factor is in the range 1.2 to 1.8. In these cases, the Rayleigh distribution will over estimate the energy yield.
This is a link to a more detailed description of the Rayleigh Distribution, it will be updated over the next few weeks as other work is completed.
Rayleigh Distribution
Friday, 28 February 2014
Clouds and Irradiance
Comment
This was written over a year ago to gather together thoughts and observations on the relationship between clouds and solar devices. It has not been formally reviewed, thus it should be treated with caution and as a discussion.
Solar Devices
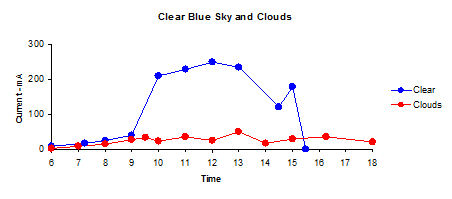
The first graph shows the current delivered to the battery between 06:00 and 18:00:
The second shows the charge supplied to the battery (in mA hours):
The "clear" and "clouds" represent the extreme cases, most days are a mix of blue sky and passing clouds.
On days when the sky state consists of a few, scattered or broken clouds there will be significant fluctuations in irradiance within a short space of time (and hence output) as can be seen in the graph below:
At the time these measurements were recorded, scattered cloud was present at an estimated height of 2 - 4,000 feet.
The Sky over Southern England
The bubble chart shows the states of the sky over southern England during a year:
The graphic does not give a full description of the sky. In summer the low cloud is typically a thin layer of cumulus which has only a moderate attenuating effect whilst in winter, the sky is overcast with a thick layer of stratus.
 |
| Summer |
 |
| Winter |
 |
| Summer |
 |
| Winter |
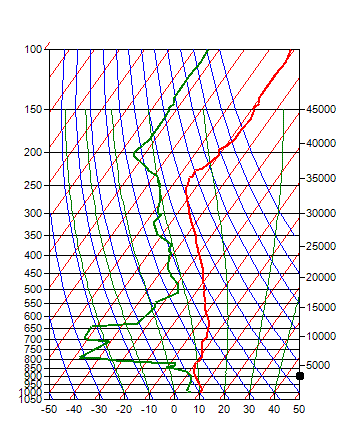
SkewT diagrams are complex, but a lot of information can be obtained visually.
When the temperature and dew point lines are far apart, the relative humidity is
low, as is the proability of cloud formation, when they are close together, the
relative humidity is high and it is probable that clouds have formed. In
the left hand diagram, the cloud is probably a thin layer of cumulus as shown in
the photo above. In winter, the high relative humidity resulting from
lower temperatures may allow can allow a thick layer of cloud to form.
Solar devices and the human body generally don't make too much
distinction between a clear blue sky and one with a few clouds in it, but a thick
overcast layer can reduce the amount of solar radiation reaching the Earth's
surface by more than 80%. This can reduce the output of solar devices and
creates a desire in the English to move closer to the Equator.
What Clouds Do
What Clouds Do
The effect of clouds is to reduce the amount of the Sun's radiant energy
transmitted to the Earth's surface. Part of the energy is reflected
upwards and part of it is absorbed within the cloud itself. This is
illustrated in the diagram below:
It shows that effect of clouds during winter is much greater than during the summer months.
Describing the effect of Clouds
There are many ways of describing the effect of clouds. Most of the comments on this site are based on the Clear Sky Factor (CSF for short), This is the ratio of the observed global horizontal iraddiance (OGH) to estimated clear sky global horizontal irradiance:
Under a clear sky, the value of CSF is constant at 1.00, under a thick, overcast sky it is usually in the range 0.1 to 0.2
The choice of GHI as a basis for a ratio is pragmatic, GHI is the most readily available form of solar irradiance data and secondly it is relatively independent of device geometry.
The second measure is the diffuse fraction which is the ratio of diffuse irradiance to total irradiance:
The diagrams below show how CSF and DF change with the state of
the sky. These diagrams are idealised, even a casual glance at a
clouded sky suggests that there is strong random element in the behaviour
of clouds and for this reason it might be desirable to model CSF and DF as
probability distributions.
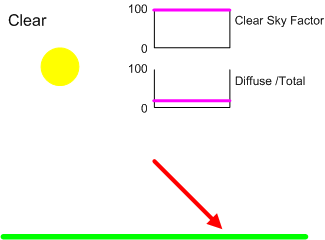
Clear Sky
Under Pure Clear Sky conditions, there is no attenuation, the value of CSF is 1.00 and the diffuse fraction in the range 0.05 – 0.15.
Overcast Sky
At the other extreme, the modal value of CSF for a thick overcast sky is around 0.2 with a relatively narrow variation, say in the range 0.1 to 0.3. No direct sunlight reaches the ground and the diffuse fraction is constant at 1.00
The Cloudy Sky
The cloudy Sky is an intermediate state between clear and overcast. A common scenario is for cloud masses to move across the sky propelled by wind. When a sensor on the ground sees clear sky, the instantaneous value of CSF is around one and the diffuse fraction will be greater than under a clear sky. It is possible in the case of FEW clouds or high level clouds that CSF will exceed one due to the additional diffuse irradiance. When the Sun is obscured by cloud, there will be little or no direct irradiance and the diffuse fraction will approach one. Over a time interval, say 15 minutes, the time average of CSF will be proportional to the amount of cloud cover.
Precipitation and Obscuration
Rain, snow and fog are frequently associated with low, dense cloud, added to which is a layer of large droplets of liquid water. The effect, depending on the intensity of the weather is to lower the value of CSF below that expected from overcast cloud, sometimes to around 0.05.
A special case of the effects of weather on solar devices is when the receiving surface becomes covered in snow, in this case the CSF falls to zero, even though pure clear sky conditions may prevail.
The effect of Height
Cloud types are divided into three groups, low, medium and high. Low clouds are those between ground level and 6,000 feet, their formation is influenced by conditions on the ground. High clouds exist above 18,000 feet and are composed of ice crystals. It is less common for medium level clouds to exist as a single layer, they are often part of a complex sky during periods of changeable weather.
Weather reports usually only provide information on the extent of the cloud and the height of the base above ground and sometimes the type (e.g. cumulus, cirrus etc.), they do not describe the thickness. The thickness can be a function of the climate type and season, for example, the description OVC020 (overcast with the base at 2,000 feet) might describe a thin layer of stratocumulus in in a Californian summer or a thick layer of nimbostratus during a European winter. Also as the extent of the lower layer increases, less is known about the layers above, thus in the example above, there could be several layers of cloud above the overcast at 2,000 feet. The comments on are based on observations of single layers of cloud and because of the issues outlines above, should be treated as generalisations. As the complexity of the sky increases, conditions become overcast.
Low cloud has the greatest attenuating effect. Skies described as having a single layer of few, scattered or broken cloud typically have CSF values in the range 0.4 to 0.6 when the sun is obscured by cloud. The length of the period of obscuration increases as as the extent increases. As the extent becomes overcast the range of CSF values can extend from 0.6 right down to less than 0.1. The lower values being associated with thick layers of stratus or nimbostratus often with bases around 1,000 feet.
In most cases, high clouds such as cirrus have a relatively small attenuating effect ,an overcast sky of high level cloud might might have a CSF value of 0.8.
 |
| Add caption |
The cloud also changes the nature of the irradiance. The cloud
acts as a diffuser, when the Sun is obscured by a cloud, the irradiance is
not only attenuated, but becomes diffuse.
The proportion of energy transmitted is a function (amongst other
things) of the type of cloud, its height and thickness, the nature and
extent of the cover and the time of day. All of which conspire to
make it difficult, if not impossible to model the process.
The Seasons
Whilst the attenuating effect of clouds is a combination of reflection and absorption, there does seem to be a link between the thickness of a cloud layer and its attenuating effect. In winter, the base of low level cloud falls and the thickness increases as does the zenith angle. The graph below was inferred from data collected by the Electric Solar Bucket in the South of England.
Whilst the attenuating effect of clouds is a combination of reflection and absorption, there does seem to be a link between the thickness of a cloud layer and its attenuating effect. In winter, the base of low level cloud falls and the thickness increases as does the zenith angle. The graph below was inferred from data collected by the Electric Solar Bucket in the South of England.
It shows that effect of clouds during winter is much greater than during the summer months.
Describing the effect of Clouds
There are many ways of describing the effect of clouds. Most of the comments on this site are based on the Clear Sky Factor (CSF for short), This is the ratio of the observed global horizontal iraddiance (OGH) to estimated clear sky global horizontal irradiance:
Under a clear sky, the value of CSF is constant at 1.00, under a thick, overcast sky it is usually in the range 0.1 to 0.2
The choice of GHI as a basis for a ratio is pragmatic, GHI is the most readily available form of solar irradiance data and secondly it is relatively independent of device geometry.
The second measure is the diffuse fraction which is the ratio of diffuse irradiance to total irradiance:
Under a clear sky, the diffuse fraction is typically around 0.15 whilst under an
overcast sky is constant at 1.00
The effect of increasing extent
Clear Sky
Under Pure Clear Sky conditions, there is no attenuation, the value of CSF is 1.00 and the diffuse fraction in the range 0.05 – 0.15.
Overcast Sky
At the other extreme, the modal value of CSF for a thick overcast sky is around 0.2 with a relatively narrow variation, say in the range 0.1 to 0.3. No direct sunlight reaches the ground and the diffuse fraction is constant at 1.00
The Cloudy Sky
The cloudy Sky is an intermediate state between clear and overcast. A common scenario is for cloud masses to move across the sky propelled by wind. When a sensor on the ground sees clear sky, the instantaneous value of CSF is around one and the diffuse fraction will be greater than under a clear sky. It is possible in the case of FEW clouds or high level clouds that CSF will exceed one due to the additional diffuse irradiance. When the Sun is obscured by cloud, there will be little or no direct irradiance and the diffuse fraction will approach one. Over a time interval, say 15 minutes, the time average of CSF will be proportional to the amount of cloud cover.
Rain, snow and fog are frequently associated with low, dense cloud, added to which is a layer of large droplets of liquid water. The effect, depending on the intensity of the weather is to lower the value of CSF below that expected from overcast cloud, sometimes to around 0.05.
A special case of the effects of weather on solar devices is when the receiving surface becomes covered in snow, in this case the CSF falls to zero, even though pure clear sky conditions may prevail.
The effect of Height
Cloud types are divided into three groups, low, medium and high. Low clouds are those between ground level and 6,000 feet, their formation is influenced by conditions on the ground. High clouds exist above 18,000 feet and are composed of ice crystals. It is less common for medium level clouds to exist as a single layer, they are often part of a complex sky during periods of changeable weather.
Weather reports usually only provide information on the extent of the cloud and the height of the base above ground and sometimes the type (e.g. cumulus, cirrus etc.), they do not describe the thickness. The thickness can be a function of the climate type and season, for example, the description OVC020 (overcast with the base at 2,000 feet) might describe a thin layer of stratocumulus in in a Californian summer or a thick layer of nimbostratus during a European winter. Also as the extent of the lower layer increases, less is known about the layers above, thus in the example above, there could be several layers of cloud above the overcast at 2,000 feet. The comments on are based on observations of single layers of cloud and because of the issues outlines above, should be treated as generalisations. As the complexity of the sky increases, conditions become overcast.
Low cloud has the greatest attenuating effect. Skies described as having a single layer of few, scattered or broken cloud typically have CSF values in the range 0.4 to 0.6 when the sun is obscured by cloud. The length of the period of obscuration increases as as the extent increases. As the extent becomes overcast the range of CSF values can extend from 0.6 right down to less than 0.1. The lower values being associated with thick layers of stratus or nimbostratus often with bases around 1,000 feet.
In most cases, high clouds such as cirrus have a relatively small attenuating effect ,an overcast sky of high level cloud might might have a CSF value of 0.8.
Friday, 21 February 2014
Mill Hill - The clue is in the name
I live on the west side of a densely populated valley in part of the country where the prevailing wind is from the south west. Occasionally, a family living on the floor of the valley embellishes a family celebration with helium filled party balloons and inevitably a few break loose from tiny hands and escape. Usually, their freedom is short lived as they get caught up in the surrounding trees but sometimes, especially on a calm day, one ascends vertically. At some height, maybe, 100m, the balloon heads off to the east.
You can learn a lot about solar irradiance from one's own backyard, but studying the wind means leaving the house. From watching lost toy balloons, hot air balloons that I hope were not lost, walking and cycling around the town and countryside with a wind speed meter and looking at data from personal weather stations, I have formed the hypothesis that wind flows reasonably steadily of over hills and humps but is attenuated and gusty in the dips in between. If wind blows up a valley, there can be a funnelling effect in which case the valley ceases to be a place of shelter. In other words wind does not always flow parallel to the surface. As always, these comments should be treated with caution as other conclusions maybe possible with wider experience and greater knowledge.
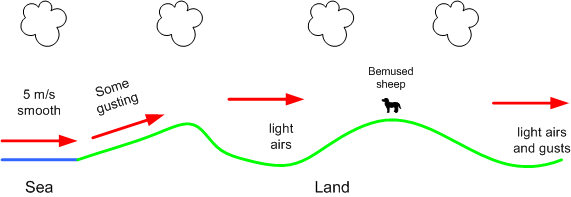
On 21-Sep-2013, I walked along a ridge from which there was a sea view, then dipped into a valley, as I walked along the path that lead to the next ridge I encountered a bemused sheep which continued to graze whilst I messed with a wind speed meter. Beyond this second ridge is an inland plain. On the seafront, the wind was blowing steadily at 5 m/s from the south west. The sketch below is an interpretation of the wind speed measurements I took along the way. On the slope up from the sea the wind blew steadily with some gusting as it did on the two ridge tops. In the valley, the air was still, with little movement in the tree tops. On the plain, there were some light gusts of wind. The red arrows suggest the path of the wind.
You can learn a lot about solar irradiance from one's own backyard, but studying the wind means leaving the house. From watching lost toy balloons, hot air balloons that I hope were not lost, walking and cycling around the town and countryside with a wind speed meter and looking at data from personal weather stations, I have formed the hypothesis that wind flows reasonably steadily of over hills and humps but is attenuated and gusty in the dips in between. If wind blows up a valley, there can be a funnelling effect in which case the valley ceases to be a place of shelter. In other words wind does not always flow parallel to the surface. As always, these comments should be treated with caution as other conclusions maybe possible with wider experience and greater knowledge.
On 21-Sep-2013, I walked along a ridge from which there was a sea view, then dipped into a valley, as I walked along the path that lead to the next ridge I encountered a bemused sheep which continued to graze whilst I messed with a wind speed meter. Beyond this second ridge is an inland plain. On the seafront, the wind was blowing steadily at 5 m/s from the south west. The sketch below is an interpretation of the wind speed measurements I took along the way. On the slope up from the sea the wind blew steadily with some gusting as it did on the two ridge tops. In the valley, the air was still, with little movement in the tree tops. On the plain, there were some light gusts of wind. The red arrows suggest the path of the wind.
I recently wrote a small programme to draw contour lines using SRTM data. Whilst this was written for some other purpose, I have used it to plot the terrain around a random selection of windmills (the sample size was 14) identified from Wikipedia. A little reading around the subject suggested that location of many mills is named "Mill Hill" (obvious with hindsight). If you Google "Mill Hill" you wind find a diverse list of places around the UK. Not all windmills are located on ridges and hills, but it is a favoured location. The graphic below shows a typical windmill location in a hilly region, the red contours are the high ground and the blue ones are the surrounding low lying area.
One source of wind data is aviation weather reports (Metars). It was whilst looking at the terrain on which airfields were located, it appeared that some which were laid out in the 1920's and 1930's are located on plateaus, like the one shown below. This observation is from a very small sample but may have some logic. A favourable wind would help getting a heavily laden and by today's standards, under powered aircraft off the ground
And my point is? The number of onshore locations where a wind turbine can be usefully be placed is constrained by terrain. This is further influenced by accessibility (almost everywhere belongs to someone) and acceptable land use.
Friday, 14 February 2014
Wind - Going off at a tangent
When I first became interested in the contribution wind and solar energy could make to a sustainable energy economy, a good starting point seemed to get an understanding of the energy available for conversion into heat or electricity. There is a lot of good wind data available in the public domain, so I started plotting out out wind speed distribution diagrams like to one below for a randomly selected group of worldwide locations.
I've had to put this work to one side for a few months, but not being the most disciplined of researchers, I wondered if the software used for the contour plots could be used to give an insight into the location of windmills. In reality, this was going off at a tangent, but the logic was that windmills are found in places for which there is no readily available source of wind speed data, thus studying their location would be an interesting way of looking at terrain and wind, this work has also been moved to one side, but I am looking forward to returning to it.
As is the way with these things, one question leads to several more. The first concerned the sample. Most "good" data is collected not amuse spreadsheet addicts, but to assist the safe passage of ships and aeroplanes which tend to operate from open, uncluttered spaces and often produce neat and tidy datasets which can be modelled with the Rayleigh or Weibull distribution (the Rayleigh distribution is a special case of the Weibull distribution in which the shape factor is constant at 2.0). Even without attracting attention to oneself by cycling around with a wind speed meter, it became clear that the wind speed distribution in places like backyards and some other parts of the urban and rural landscape where more complex.
Terrain is a factor in determining the amount of wind energy available at a given location. The average wind speed and distribution will be different at the floor of a valley from that at the ridges either side. These comments are drawn from work in progress from which as yet no definite conclusion as been drawn, thus they should be treated with caution. In general, offshore wind polewards of the tropics has a higher average speed than onshore and approximates to a Weibull distribution with a shape factor of 2.0. Onshore at a similar latitude, the average wind speed is lower than offshore and its distribution more skewed to the left, in terms of the Weibull distribution, the shape factor is often in the range 1.3 to 1.8, the higher values being associated with flat, open areas.
In an attempt to explore the effects of terrain on the distribution of wind speed, I plotted small contour maps using data from the SRTM mission, like the one shown below which is centred on a windmill close to where I live..
Terrain is a factor in determining the amount of wind energy available at a given location. The average wind speed and distribution will be different at the floor of a valley from that at the ridges either side. These comments are drawn from work in progress from which as yet no definite conclusion as been drawn, thus they should be treated with caution. In general, offshore wind polewards of the tropics has a higher average speed than onshore and approximates to a Weibull distribution with a shape factor of 2.0. Onshore at a similar latitude, the average wind speed is lower than offshore and its distribution more skewed to the left, in terms of the Weibull distribution, the shape factor is often in the range 1.3 to 1.8, the higher values being associated with flat, open areas.
In an attempt to explore the effects of terrain on the distribution of wind speed, I plotted small contour maps using data from the SRTM mission, like the one shown below which is centred on a windmill close to where I live..
I've had to put this work to one side for a few months, but not being the most disciplined of researchers, I wondered if the software used for the contour plots could be used to give an insight into the location of windmills. In reality, this was going off at a tangent, but the logic was that windmills are found in places for which there is no readily available source of wind speed data, thus studying their location would be an interesting way of looking at terrain and wind, this work has also been moved to one side, but I am looking forward to returning to it.
Wikipedia has some excellent lists of windmills from around the United Kingdom, and in may cases does the tedious task of converting National Grid coordinates to lat/lng relative to the WGS84 datum which are compatible with the SRTM data.
Windmills are part of the English landscape, especially in the eastern counties, but I was surprised at the number of them, maybe 2,000 (a guess) with the majority being built and operated in the 19th Century. At the beginning of the 20th century, the windmills were displaced by factories powered by steam, oil or electricity. For there to be so many windmills in operation, there must have been a substantial industry dedicated to their construction and maintenance together with a knowledge of the relationship between terrain an wind energy, I would be curious to know if there was a reference work on this?
In a week in which the UK has been lashed by some of the most violent storms in living memory, it should be remembered that the wind machinery has to survive under considerably harsher conditions than it normally operates. In storm conditions, wind turbines shut down in an attempt to minimize the risk of damage.
Windmills are part of the English landscape, especially in the eastern counties, but I was surprised at the number of them, maybe 2,000 (a guess) with the majority being built and operated in the 19th Century. At the beginning of the 20th century, the windmills were displaced by factories powered by steam, oil or electricity. For there to be so many windmills in operation, there must have been a substantial industry dedicated to their construction and maintenance together with a knowledge of the relationship between terrain an wind energy, I would be curious to know if there was a reference work on this?
In a week in which the UK has been lashed by some of the most violent storms in living memory, it should be remembered that the wind machinery has to survive under considerably harsher conditions than it normally operates. In storm conditions, wind turbines shut down in an attempt to minimize the risk of damage.
Labels:
economics,
Energy,
Renewables,
sustainability,
Wind
Subscribe to:
Posts (Atom)